Curves of ZoKrates

13 minute read

Curves

ZK toolboxes facilitate the process of constructing circuits compatible with SNARK proving systems. Their primary goal is to provide high level interfaces and programming syntax that are familiar and accessible to a broad spectrum of users, abstracting away the underlying complexities of circuits, curves, and cryptography.

For various reasons certain semantics of the proving system remain visible in ZK toolboxes and require a certain level of familiarity with them. Take for example the field data type that occurs in ZoKrates and other DSLs. It is a special data type that in some cases behaves like an unsigned integer, often leading to misconception that fields and integers can be used interchangeably.

To demonstrate, consider the following two ZoKrates programs that divide x and y and output the result:

// ZoKrates Program 1
def main() -> u32 {
	u32 x = 5;
	u32 y = 2;
    u32 z = x / y;
    return z;
}

// ZoKrates Program 2
def main() -> field {
	field x = 5;
	field y = 2;
	return x / y;
}

In the first program, the numbers are of type u32 and the program outputs 2. The second program they are of type field, producing the output 10944121435919637611123202872628637544274182200208017171849102093287904247811.

Where this value comes from, what the field data type means, and what its appropriate usage is are the subjects of this post.

We will look at:

Groups, Fields, and Elliptic Curves
Elliptic Curves underlying ZoKrates, in particular BabyJub and BN128, and their relation to the Field data type
Embedded Curves and the role they play in SNARKs
An End to end digital signature example, showing the interplay of elements in signature generation, proof generation, and proof verification.

Groups and Fields

According to ZoKrates’ official documentation:

Field is the most basic type in ZoKrates, and it represents a field element with positive integer values in [0, p - 1] where p is a (large) prime number.

To shed more light on the meaning of the statement, this section explains the groups and fields algebraic structures.

Groups

A group is a set of values together with a group operation (like addition or multiplication) that follows a few simple rules:

Closure. If you take any two values from the group and apply the group operation, the result is also in the group. Think of it like a function that never returns an “out-of-bounds” value.

Associativity. The order in which you group operations does not matter. So for example (a + b) + c is the same as a + (b + c).

Identity. There’s a special value in the group (called the identity) that does not change anything when used as operand in the operation. Like adding 0 to a number, or multiplying by 1 - the result stays the same.

Inverses. For every value in the group, there exists another value (called its inverse) such that when you apply the group operation between them, you get the identity value. Think of it like this: If a * b = identity, then b is the inverse of a.

Fields

Field is a powerful structure that supports two operations simultaneously (usually addition and multiplication), each with their own group-like behavior that interact nicely with one another. Thus, it is a set of values with the following 2 main rules:

1. Addition forms a group. Just like the group definition, this means the field elements together with the addition operator + have:

Closure
Associativity
Identity value is 0 (a + 0 = a for every group element a)
Inverses (every element a has -a such that a + (-a) = 0
Often also commutative, i.e., a + b = b + a

2. Multiplication (excluding 0) forms a group. All non-zero elements together with the multiplication operator * have:

Closure
Associativity
Identity value is 1 (a * 1 = a for every group element a)
Inverses: For any a ≠ 0, there is b = 1/a such that a * b = 1
Often also commutative: a * b = b * a

The group also has multiplication distributivity: a * (b + c) == a * b + a * c

Groups and fields build the Elliptic Curves used in constructing zero knowledge proofs.

Fields of ZoKrates

In ZoKrates, the field data type is nothing but an implementation of the Field definition above. Variables of type field may then take any number in the set of integers from 0 to p-1 where p = 21888242871839275222246405745257275088548364400416034343698204186575808495617. In this set, the addition operators (+, -) form an additive group, and the multiplication operators (*, /) form a multiplicative one, i.e., all arithmetic operations on field variables are performed modulo p, thus all outputs remain inside the group (closure). Note that division is just a multiplication by the multiplicative inverse.

To demonstrate, observe the following python program:

p = 21888242871839275222246405745257275088548364400416034343698204186575808495617
x = 5
y = 2
inverse_ y = pow(y, -1, p)
result = x * inverse_y
print(result)

Running this program outputs 10944121435919637611123202872628637544274182200208017171849102093287904247811, which matches exactly the ZoKrates program in the Introduction.

By now you should have an understanding of how arithmetic operations on field elements differ from integers. But why does p take this particular value? To answer this question, we need to take a look at elliptic curves and explain their relation to fields and groups.

Brief Overview of Elliptic Curves

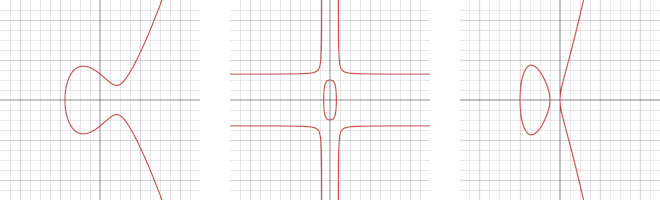
In Elliptic Curve Cryptography, an Elliptic Curve is commonly represented by the mathematical equation $y^2 \equiv x^3 + ax + b \mod p$ for some constant $a$ and $b$, where the $(x,y)$ are all points on the curve, i.e., satisfying this equation. This type of equation is also called the Weierstrass form and is typically visualized as follows:

Image of Weierstrass Curve

Elliptic Curves that are useful to Cryptography are those that have a large number of its points form a Group, where the group elements are points on the curve and the arithmetic operation is addition. In this case, there are algorithms for executing the arithmetic group operations over points on the curve such adding two points, doubling a point, and multiplying a point with a scalar (non-point) value, i.e, repeated addition of a point to itself.

Curve Properties

An elliptic curve carries the following set of properties:

Curve Order $n$: A curve order is the total number of points on the curve, i.e., the set of all $(x,y)$ that satisfy the curve equation.

Base Field $q$: Describes a finite field $\mathbb{F}_q$ over which the curve is defined, i.e., from which all values $x$ and $y$ are taken. $q$ is then the number of elements in that field.

Scalar Field $r$: For cryptographic operations on Elliptic curves to be secure, they must be performed within a large group of prime order (size). If the curve’s order is already prime, then this group contains all points on the curve, thus $r = n$. If, on the other hand, the curve’s order is a composite, then we are operating within a subgroup of order $r < n$, i.e., within a subset of the points on the curve whose size is a large prime $r$.

Generator: A point on the curve that can generate all other points via successive addition of the point to itself, and referred to as the primitive element. If the group order is prime, then all points except the point at infinity are generators.

Advanced Curves

In addition to the Weierstrass form, there are other methods to describe curves where they are represented via different equations and algorithms for the arithmetic operations, and may enable useful features.

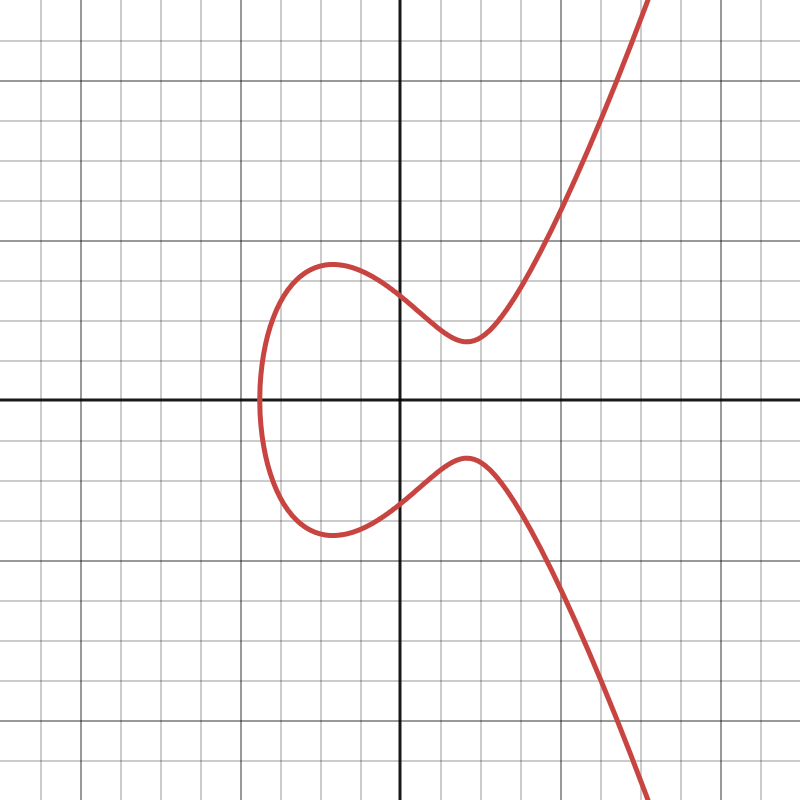
Montgomery Curves

Image of Montgomery Curve

These are well suited for fast scalar multiplication by making use of the Montegomery ladder algorithm, but are also more resistant to side-channel attacks. These curves are represented by the following equation:

\[By^2 = x^3 + Ax^2 + x\]

Prominent examples are the Curve25519 and Curve448 used in Diffie-Hellman key exchange protocols.

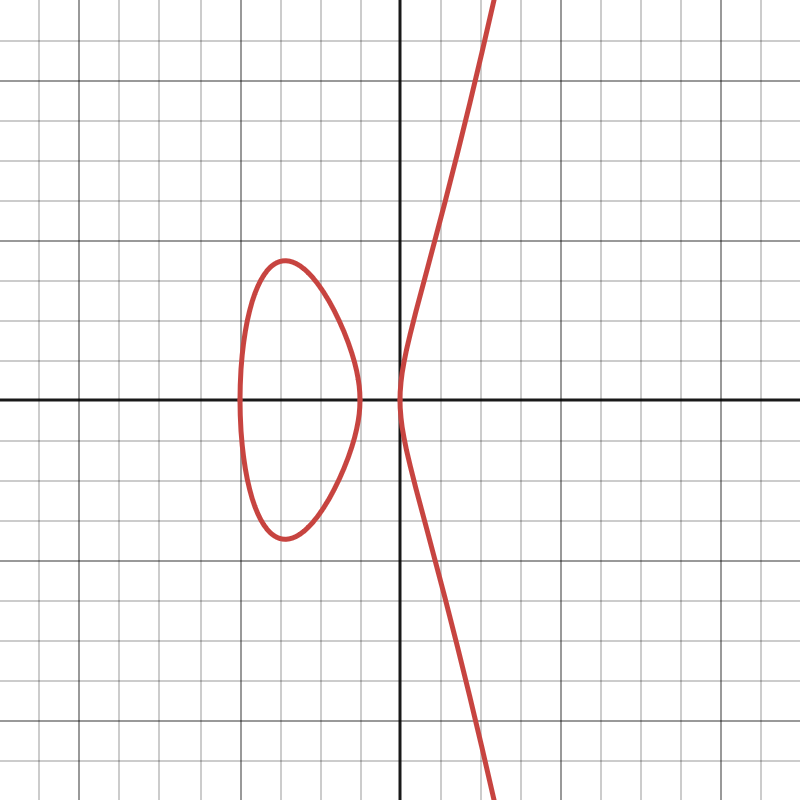
Edwards Curves

Image of Edwards Curve

Edwards curves are another interesting form of elliptic curves with different properties, represented by:

\[Ax^2 + y^2 = 1 + Dx^2 \times y^2\]

They possess a full addition law meaning that point addition has no special case (e.g., for identity element).

They also have unified addition meaning both point addition and doubling follow the same formulas. This makes it both simpler in implementation and side-channel resistant as there are no special cases to handle.

Twisted Edwards Curves

Image of Twisted Edwards Curve

Generalization of Edwards curves that include a special affine transformation that makes the curve “twisted”, and more efficient for certain mapping operations. Because of a birational equivalance relation between Montgomery and Twisted Edwards curves, it is common to first begin by specifying a Montgomery curve then transform it to a twisted Edwards form.

Pairing-friendly Curves

Pairing-based Cryptography is a branch of cryptography that is based on elliptic curves that support a special operation called pairing.

Pairing is a function $e : G_1 \times G_2 \to G_3$, i.e., a mapping from pairs of elements from 2 source groups onto a target group $G_3$. The groups are of prime order and the pairing function is bilinear. Pairing friendly curves are then curves that contain sub-groups $G_1, G_2$ and a efficient mapping to a secure, target group $G_3$. These constitute the backbone of prominent proving systems such as Groth16.

Elliptic Curves for SNARKS

A SNARK typically consists of a proving system and a process of compiling a program into something the proving system can work with. The compilation procedure involves encoding the program as a series of arithmetic operations over some Field $\mathbb{F}_r$, called an arithmetic circuit. A proving system like Groth16 can then generate proofs out of this representation.

Circuit vs Pairing-friendliness

Although verification of SNARKs is cheap (by definition of Succinctness), proof generation depends on the size of the circuit and can be very costly. The size of the circuit (and in turn, the proof computation cost) is particularly amplified when the statement to be proven involves field or Elliptic Curve arithmetic, which typically appears in cryptographic operations such as verifying a digital signature.

Hence, two primary scalability factors directly impact circuit size:

Complexity of field and elliptic curve arithmetic operations (addition, multiplication, ..etc)
Whether the field is native to the proving system.

If the arithmetic operations are expensive, for example due to having to handle special cases, it results in more complex circuit representation. If the field itself in which the arithmetics take place is not compatible with the proving system’s field (non-native), the target field needs to be simulated, producing prohibitively expensive circuits.

The first can be addressed by restricting the proving to statements (e.g., signature validity) over Twisted-Edwards curves in order to make use of efficiency gains of full and unified addition properties. Twisted-Edwards curves are therefore often referred to as circuit-friendly curves. Groth16 proving system, however, requires a pairing-friendly curve due to the use of pairings. Unfortunately, pairing-friendly curves are not great for efficient arithmetization, and it turns out there are no curves that are both circuit and pairing friendly at the same time. So how can we have the best of both worlds? Embedded Curves!

Embedded Curves

An embedded curve is an Elliptic Curve defined over the scalar field of another curve, that is, if $E_1$ is an elliptic curve embedded within another Elliptic curve $E_2$, then $E_1$’s base field equals $E_2$’s scalar field. Intuitively this means that if $(x,y)$ is a point on $E_1$, then $x$ and $y$ are valid scalars in $E_2$. This notion is also referred to as chaining and it addresses the other scalability challenge: statements in the base field of $E_1$ are also in the scalar field of $E_2$, thus native to the proving system.

Groth16-based implementations of SNARKS thus harness the efficiency benefits of chaining by supporting the expression of statements to prove on a circuit-friendly curve (called the proving/inner curve) which is embedded on a pairing-friendly curve for verification (called the verification/outer curve).

Putting Everything Together

Groth16 is an efficient proving system that operates on arithmetic circuits and requires a pairing-friendly curve
Converting a computation into an arithmetic circuit is best done on circuit-friendly curves for efficiency
Embedded curves enable compatibility of the circuit-friendly with the pairing-friendly curve

ZoKrates supports multiple curves for compatibility with multiple blockchains. For Ethereum, it uses the Twisted-Edwards curve BabyJubJub as the proving curve, which is embedded on the pairing friendly BN128 curve- a curve natively supported by Ethereum. ZoKrates also supports further pairing-friendly curves like BLS12_381, BLS12_377, BW6-761, unfortunately with no yet support for respective embedded curves in the standard library.

In the next section, we look at a ZoKrates example employing BabyJubJub and its corresponding BN128 curve.

End to End Example

To conclude this post, we look at a real-world case that puts everything together in a practical example.

An common scenario that happens to demonstrate the interplay between all the components conveyed in this post is proving the validity of a digital signature. Namely, you will see that

Key generation and signing process take place on BabyJubJub
The statement to prove (signature validity) is expressed on the inner curve - BabyJubJub
The generated proof is verified in an Ethereum smart contract over the outer curve - BN128

Luckily, we have already blogged about signature generation and verification, so rather than repeating, we will expand on the existing post and bring it into context.

Verifying Digital Signatures

First, familiarize yourself with the signatures blog post and notice the following:

In python, the signature is generated over the BabyJubJub elliptic curve, which is a twisted Edwards Curve.
The signature produced is a point on the BabyJubJub curve $R = (x, y)$ and a scalar $s$, indicating that $x$ and $y$ are in the base field of BabyJubJub.
ZoKrates takes the coordinates $(x,y)$ as inputs of type field, showing that ZoKrates’ field data type is for expressing statements over elements in the base field of BabyJubJub.

Now go ahead and generate the solidity verifier by running zokrates export-verifier and observe the following code chunks in the generated Verifier.sol:

Verification function takes a Proof object:

// L203-205
function verifyTx(
        Proof memory proof, uint[17] memory input
    ) public view returns (bool r) {

The proof consists of elliptic curve points in some groups G1 and G2:

// L9-17
struct G1Point {
    uint X;
    uint Y;
}

struct G2Point {
    uint[2] X;
    uint[2] Y;
}

// L155-159
struct Proof {
    Pairing.G1Point a;
    Pairing.G2Point b;
    Pairing.G1Point c;
}

G1 and G2 are associated to BN128 curve, evident by the staticcall line to a precompiled contract address 7, which performs scalar multiplication for that curve (see EIP-196):

// L58..65
function scalar_mul(G1Point memory p, uint s) internal view returns (G1Point memory r) {
    uint[3] memory input;
    input[0] = p.X;
    input[1] = p.Y;
    input[2] = s;
    bool success;
    assembly {
        success := staticcall(sub(gas(), 2000), 7, input, 0x80, r, 0x60)

And finally, if you observe the verification logic, you will easily find usage of pairing.

Summary

We have taken a look at some of the mathematical structures that enable SNARKs, mostly abstracted away by high-level DSLs such as ZoKrates. In particular, we focused on the field data type that often occurs in these DSLs which - without background knowledge - may seem to possess peculiar behaviour. We covered an end-to-end verification of digital signature example in which one the role of field elements in signature generation, proving, and verification is observable.

Resources and Further Readings

BN128 Curve Parameters

Curve Order = 21888242871839275222246405745257275088548364400416034343698204186575808495617
Scalar Field = 21888242871839275222246405745257275088548364400416034343698204186575808495617 (same like order)
Base Field (modulus) = 21888242871839275222246405745257275088696311157297823662689037894645226208583
Generator of G1 = (1, 2)
Generator of G2 = ( x = (11559732032986387107991004021392285783925812861821192530917403151452391805634, 10857046999023057135944570762232829481370756359578518086990519993285655852781), y = (4082367875863433681332203403145435568316851327593401208105741076214120093531, 8495653923123431417604973247489272438418190587263600148770280649306958101930))
Type-3 pairings (G1 != G2)

Baby JubJub Parameters

Scalar Field = 2736030358979909402780800718157159386076813972158567259200215660948447373041
Base Field (modulus)= 21888242871839275222246405745257275088548364400416034343698204186575808495617
Cofactor = 8
Twisted Edwards

Share on

Twitter Facebook LinkedIn