Merkle Proofs with ZoKrates
Merkle Proofs and zkSNARKs provide a powerful instrument to enrich (decentralized) applications, e.g., through non-disclosing membership proofs. In this post, you will learn:
- How Merkle Proofs can be constructed from Merkle Trees.
- How zkSNARKs enrich Merkle proofs with privacy guarantees and it’s application.
- How Merkle Proofs can be implemented with ZoKrates.
Remarks
We assume basic knowledge of zkSNARKs, hashing, and ZoKrates that can be gained from our basic tutorials. All the material used in this tutorial can be found in our tutorials repository. Please note that all the source code displayed on this page was compiled using ZoKrates 0.8.6. We do not guarantee its compatibility with future versions.
Merkle Trees and Proofs
Merkle Trees are binary trees where each non-leaf node is the hash of its child nodes, and the leaf nodes contain the hash of data blocks. In this hierarchical structure, the root node, also known as the Merkle Root, is the hash of all the underlying data, providing a unique fingerprint. The depth of the Merkle Tree, an essential aspect of its structure, refers to the length of the longest downward path from the root to a leaf.
Merkle Proofs, on the other hand, are procedures used to validate the integrity of data chunks in the Merkle Tree. A Merkle proof, in essence, verifies the existence of a specific data element within a larger Merkle Tree. First, we start with the data element for which we want to generate or verify a proof. This data element is located at a leaf node of the Merkle Tree. To generate a proof, we need to provide the hashes of the sibling nodes along the path from this leaf that result in the Merkle Root. In a balanced binary tree the size of the Merkle Proof is equal to the depth of the Merkle Tree.
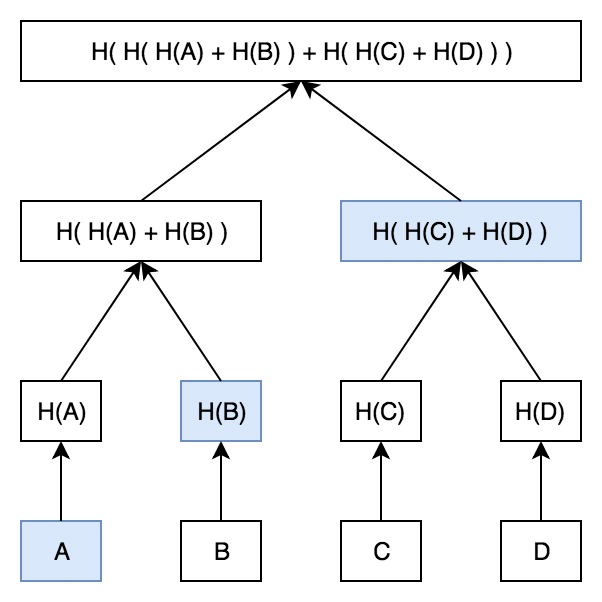
Merkle Tree with an example Merkle Proof (blue)[1]
To verify the proof, we start by hashing the data element in question. The resulting hash is then iteratively hashed together with the sibling hashes on the different tree levels following the structure of the tree. The collection of the sibling hashes needed to arrive to the Merkle Root, is also called Merkle Path. This process needs to be done in the correct order, that is starting with the lower level, and specificing the correct order of the sibling hashes, whether left or right. We continue this process until we reach the top of the tree. If the final computed hash matches the Merkle Root of the tree, the proof is valid, and we can be sure that the data element is indeed part of the original dataset. If the hashes do not match, then the proof is invalid.
The power of Merkle proofs lies in their efficiency. Given a binary tree with n leaf nodes, constructing a Merkle Tree involve calculating 2n hashes (n + n/2 + n/4…), while the size of a proof is proportional to the tree depth, which is log(n). Because a Merkle Proof can be verified in logarithmic time, even big Merkle Trees managing vast amounts of data can be verified efficiently. For this reason, Merkle Trees and Proofs are suitable tools for decentralized and distributed systems like blockchains, where computational efficiency and data integrity are crucial.
Merkle Proofs with ZKPs
Merkle proofs can be enriched through privacy guarantees if executed inside a zkSNARKs. zkSNARKs allows to prove the possession of a valid Merkle Proof without disclosing the candidate element or the Merkle Path. Here are some examples of zk-proofs that can be made with Merkle Proofs and their applications:
Membership proof:
- Merkle proofs enable demonstrating that a certain element is a part of a given set without revealing which element it is. The Merkle Tree stores a list of elements, and the zkSNARK is used to prove knowledge of a path from a leaf element to the root of the Merkle Tree. By executing the Merkle Proof inside a zkSNARK, the candidate element and the Merkle path can be kept private. Such membership proofs can be used in zkRollups to demonstrate that sender and receiver addresses of a transaction contained in a rollup are part of a set of registered blockchain accounts. Since the addresses are typically treated as public inputs, here, the zero-knowledge property is not crucial. Identity proofs is another application where a membership proof can be used privacy-preserving credential systems. This can be done by storing hashed data in a Merkle Tree, where each leaf represents a user’s hashed credential. zk-SNARK can then be used to prove that a user knows the pre-image of a hash in the tree, which would prove their credential.
Range proof:
- A range proof is a demonstration that a certain number falls within a specific range. This is usually done by structuring the data in the Merkle Tree in a specific way (like sorted order) and then using zk-SNARKs to prove that for any two adjacent elements, the non-member value is greater than the smaller one and less than the larger one. In other words, the proof shows that the non-member value would have been between these two values if it were in the set. A range proof can be used to build a location proofs to demonstrate that a location is within a predefined region. Here, leaves of the Merkle Tree represent the boundaries of a predefined set of ZIP codes. If the given ZIP code is within the boundary, it proves that the location is within the predefined regine, while the location itself can be kept private.
Non-membership proof:
- Just as you can prove membership, you can also prove non-membership; that is, you can prove that a certain element is not a part of a given set. This might be used, for example, to show that a particular transaction has not occurred. This is typically harder to achieve than membership proof. It is not straightforward to prove that something does not exist in a set without going through all the elements. One approach to perform a range proof, where the non-member value is greater than the smaller one and less than the larger one. In other words, the proof shows that the non-member value would have been between these two values if it were in the set.
Merkle Proofs in Zokrates
Finally, we will now see how to construct a Merkle Proof in ZoKrates a given Merkle Tree. Taken from ZoKrates cli’s examples, the following ZoKrates code assert the validity of a Merkle Proof for a Merkle Tree of depth 3:
import "hashes/sha256/512bitPadded" as sha256;
// leave the root out of the struct as all the variables
// in the struct are all private and the root is public
struct MerkleTreeProofStruct<DEPTH> {
u32[8] leaf;
bool[DEPTH] directionSelector;
u32[DEPTH][8] path;
}
// directionSelector => true if current digest is on the rhs of the hash
def select(bool condition, u32[8] left, u32[8] right) -> (u32[8], u32[8]) {
return (condition ? right : left, condition ? left : right);
}
// Merkle-Tree inclusion proof for tree depth <DEPTH> using sha256
def merkleTreeProof<DEPTH>(u32[8] root, MerkleTreeProofStruct<DEPTH> proof) -> bool {
// Start from the leaf
u32[8] mut digest = proof.leaf;
// Loop up the tree
for u32 i in 0..DEPTH {
(u32[8], u32[8]) s = select(proof.directionSelector[i], digest, proof.path[i]);
digest = sha256(s.0, s.1);
}
return digest == root;
}
const u32 TREE_DEPTH = 3;
def main(u32[8] treeRoot ,private MerkleTreeProofStruct<TREE_DEPTH> proof) {
assert(merkleTreeProof(treeRoot, proof));
}
The above code snippet can be reutilized to assert the correctness of any Merkle Tree by adjusting the TREE_DEPTH constant.
Below, is an example python-script generating a valid Merkle Proof for the above ZoKrates program:
import hashlib
def hash(value: bytes) -> bytes:
return hashlib.sha256(value).digest()
def hash_to_u32(val: bytes) -> str:
M0 = val.hex()[:128]
b0 = [str(int(M0[i:i+8], 16)) for i in range(0,len(M0), 8)]
return " ".join(b0)
if __name__ == '__main__':
original_data = [1337, 7, 1989, 51966, 1234, 9999, 0, 6]
hashed_leafs = [hash(int.to_bytes(leaf, 64, "big")) for leaf in original_data]
h0 = hash(hashed_leafs[0] + hashed_leafs[1])
h1 = hash(hashed_leafs[2] + hashed_leafs[3])
h2 = hash(hashed_leafs[4] + hashed_leafs[5])
h3 = hash(hashed_leafs[6] + hashed_leafs[7])
h00 = hashlib.sha256(h0 + h1).digest()
h01 = hashlib.sha256(h2 + h3).digest()
root = hashlib.sha256(h00 + h01).digest()
directionSelector = "1 0 0"
path = " ".join([hash_to_u32(node) for node in [hashed_leafs[0], h1, h01]])
print(hash_to_u32(root) + " " + hash_to_u32(hashed_leafs[1]) + " " + directionSelector + " " + path)
Summary
This post discussed the fundamentals of Merkle Trees and Merkle Proofs, their advantages, various types and applications, and how they interact with zk-SNARKs. The post also delved into using ZoKrates to construct a Merkle proof for a Merkle Tree.
Merkle Trees are tamper-proof binary trees where each node is the hash of its child nodes, providing a unique data fingerprint. Merkle Proofs validate the existence of a data element within a Merkle Tree.
Merkle Trees can also be combined powerfully with zkSNARKs, which are used for preserving data privacy during proof generation and verification. ZoKrates can be used to construct Merkle proofs from a given Merkle Tree, ensuring the validity of the data. The post concludes with a code snippet demonstrating how to assert the correctness of any Merkle Tree in ZoKrates, showcasing its practical use.
Sources
[1] Konstantopoulos, Georgios. (2019). Plasma Cash: Towards more efficient Plasma constructions.
Leave a comment